Il Problema

Mi sono imbattuto in questo interessante e “semplice” problema di statistica (sarebbe meglio dire dalla semplice formulazione). Questo mio post e’ in pratica una riassunto di questo bel video di Zach Star, a cui aggiungo qualche considerazione personale.

Un’osservazione: e’ molto importante la definizione della domanda che verra’ posta, perche’ ci sono vari dettagli che possono sfuggire.

Vedremo inoltre una cosa molto interessante, non e’ sufficiente pensare in termini di popolazioni, ma e’ necessario pensare anche in termini di come queste popolazioni vengono misurate.

infoSupponiamo di incontrare una persona in un bar, Tizio per gli amici. Durante una conversazione, Tizio ci dice che ha 2 figli (senza specificarne il sesso), decide poi di darci due informazioni aggiuntive, una dopo l’altra:

info1. almeno uno dei figli e’ femmina

info2. sua figlia Jane (come la morosa di Tarzan) guida il trattore.

error Domanda 1: quando il nostro interlocutore ci ha detto di avere almeno una figlia femmina quale probabilita’ esiste che anche il secondo figlio sia una femmina?

error Domanda 2: quando aggiunge che la propria figlia si chiama Jane, la probabilita’ che il secondo figlio sia femmina cambia?

Probabilita’

Prima di procedere bisogna dare una definizione operativa di probabilita'. Ne prendiamo una ragionevole e semplice (di tipo frequentista). Supponiamo che la situazione appena descritta si ripeta molte volte: incontro molti padri di famiglie diverse che mi dicono: ho due figli di cui almeno una figlia femmina. Aumento di 1 sul taccuino il numero di famiglie con almeno una femmina; in seguito annoto sul taccuino anche il sesso dell’altro figlio. Quando ho una popolazione abbastanza grande (migliaia di casi), conto il numero di famiglie totali e conto quante di esse hanno 2 femmine. La probabilita' sara’ il rapporto tra le famiglie con 2 femmine sul totale delle famiglie annotate.

Il tutto va ripetuto anche nel caso in cui il genitore ci dice di avere 2 figli, di cui almeno una femmina di nome Jane, segnandoci la famiglia e il sesso del secondo figlio. La probabilita’ sara’ anche in questo caso il numero dei casi favorevoli rispetto ai totali. Chiaramente l’insieme di famiglie con due figli, di cui uno femmina di nome Jane, e’ un sottoinsieme di quello con due figli di cui uno femmina.

Attenzione: teniamo 2 conti separati per i due casi (potremmo usare due taccuini separati).

Popolazione A

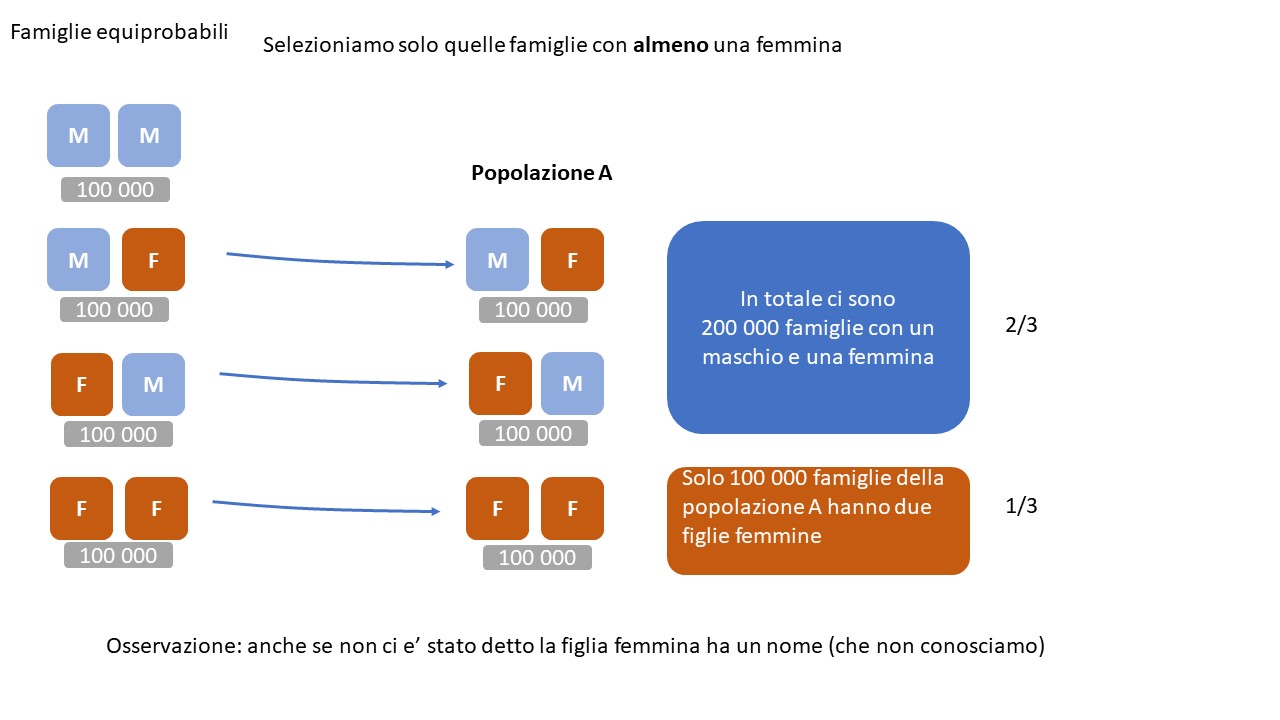
A questo punto il bravo statistico comincia a costruire un modello in cui ci sono tutti gli oggetti possibili (meglio se questi sono equiprobabili, cosi’ basta contarli). In questo caso parliamo di popolazioni e di famiglie equiprobabili.

Le combinazioni di famiglie equiprobabili sono le seguenti (M=maschio, F=femmina):

• MM (primogenito= maschio, secondogenito= maschio)
• MF (primogenito= maschio, secondogenito= femmina)
• FM (primogenito= femmina, secondogenito= maschio)
• FF (primogenito= femmina, secondogenito= femmina)

Questo perche’ possiamo considerare che all’incirca ci sia il 50% di probabilita’ di avere un figlio maschio e altrettanto di avere una femmina (inoltre il sesso del secondo figlio non e’ influenzato dal sesso del primo figlio, resta il 50%)

L’insieme delle famiglie che comprende almeno una figlia femmina e’ un sottoinsieme del totale. Chiamiamo questo sottoinsieme popolazione A, restano solo i casi:

• MF
• FM
• FF

Ognuna di questi tipi di famiglie ha la stessa probabilita’ dell’altra. Data questa popolazione (2 figli, di cui almeno una femmina), possiamo dire che solo in 1/3 dei casi la seconda figlia sara’ femmina.
Si noti che questo risultato e’ indipendente dal nome dei ragazzi.

Popolazione B

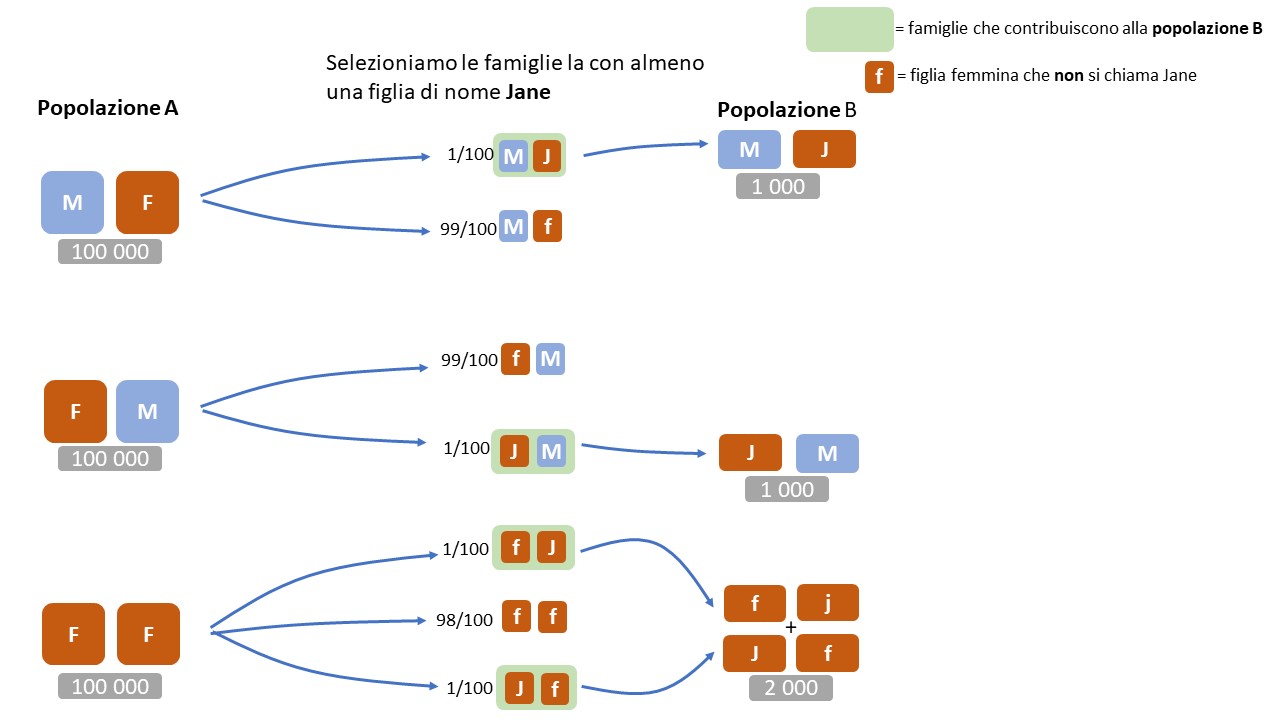
Cerchiamo ora la popolazione di famiglie per cui si ha almeno una figlia femmina di nome Jane. Questa popolazione, sara’ un sottoinsieme della popolazione A.

Per facilitarci le idee, assegnamo delle quantita’ alle popolazioni. Per esempio ci sono 100 000 famiglie MF, 100 000 FM e 100 000 FF. Supponiamo che la frazione di ragazze chiamate Jane sia 1/100.

Vediamo qual’e’ ora la popolazione di riferimento (popolazione B):

• si passa da 100 000 famiglie MF $\rightarrow$ 1000 famiglie del tipo MJ (dove J sta per Jane)
• si passa da 100 000 famiglie FM $\rightarrow$ 1000 famiglie del tipo JM
• dalle 100 000 famiglie FF $\rightarrow$ si passa a famiglie del tipo JF e FJ, quindi in totale 2000 famiglie con 2 femmine hanno una ragazza chiamate Jane.

(nel grafico sono state sottolineate in verde le famiglie che contribuiscono alla popolazione totale) In questo caso quindi la popolazione totale comprende 4000 famiglie che corrispondono alle caratteristiche: 2 figli di cui una femmina di nome Jane (supponiamo inoltre che i due figli non possano avere lo stesso nome). A differenza del caso precednte 1/2 delle famiglie comprendera’ una seconda figlia femmina.

Paradosso

Un momento:

• se conosco il nome della ragazza questo cambia in modo consistente la probabilita' che l’altro figlio sia una femmina: si passa da 1/3 a 1/2.
• Il cambio e’ indipendente dal nome della ragazza!
• quando Tizio mi aveva detto di avere una figlia, io sapevo gia' che questa doveva avere un nome… solo non sapevo quale!

Queste tre condizioni sembrano in qualche modo contradditorie. Se il passaggio da 1/3 ad un 1/2 e’ indipendente dal nome, dato che io sapevo gia’ che la ragazza aveva un nome, come e’ possibile che il fatto che mi venga comunicato cambi le probabilita? La probabilita’ o e’ indipendente dal nome, o dipende!

Soluzione: a cosa corrispondono le probabilita’ 1/3 e 1/2?

Il problema e’ molto semplice: le probabilita’ 1/3 e 1/2 non corrispondono al problema iniziale! Queste probabilita’ sono corrette se si campionano le popolazioni in un modo differente rispetto a quello enunciato dal problema. Vediamo ora un modo per ottenere quelle probabilita’. Prendiamo un campione rappresentativo di genitori con 2 figli e mettiamolo in uno stadio. A questo punto si chiede a tutti quelli con 2 figli maschi di uscire.

• Si chiede a quelli con due figlie femmine di alzare la mano. E si ottiene 1/3 del totale dei presenti.

Se invece, facciamo uscire dallo stadio tutti i genitori, tranne quelli che hanno almeno un figlio femmina chiamato Jane, e a questo punto chiediamo loro di alzare la mano se hanno anche una seconda figlia femmina, otterremo che circa 1/2 dei presenti alzera’ la mano.

Ora inserisco una piccola digressione. Esiste un interessante teorema che indica che per un “metodo di scelta random” la media spaziale (ovvero in questo caso contare tutte le famiglie con una caratteristica) puo’ essere rimpiazzata da una media temporale, a patto proprio che il criterio di scelta delle famiglie sia sufficientemente “caotico/random”. Per questo posso ottenere lo stesso risultato indicato sopra se io chiedo a tutte le persone che incontro al bar, una dopo l’altra (supponendo che siano sinceri, ovviamente):

• se hanno 2 figli di cui almeno uno femmina
• se il hanno una figlia chiamata Jane

Se uno guarda al problema dal punto di vista delle persone presenti allo stadio, il fatto di fare uscire dallo stadio tutti coloro che non corrispondono a “avere una figlia femmina” ha un effetto tangibile. Quando si chiede di uscire a tutti coloro che non corrispondono ad “avere una figlia femmina chiamata Jane” l’effetto sara’ diverso. Vengono fatti dei campionamenti differenti dalla popolazione iniziale e questo modifica quindi le frazioni/probabilita’.

errorAttenzione: il modo di procedere appena esposto non corrisponde al problema iniziale!

Il problema iniziale era invece: incontro Tizio ad un bar, ad un certo punto lui mi dice di avere due figli, di cui almeno una femmina e successivamente ci dice il nome della femmina: Jane.

In questo caso il campionamento delle popolazioni e’ fatto in modo differente! Sono i vari possibili “Tizio” che incontro al bar che definiscono il campione. Questo cambia molto il risultato. Vediamo come:

Popolazione C

Supponiamo che ogni padre abbia piu’ o meno la stessa probabilita’ di parlare dei propri figli (non e’ necessariamente vero ma e’ ragionevole), prendiamo ora la popolazione A e vediamo come si modifica, con un campionamento spontaneo (e’ il genitore che decide di cosa parlare):

• da 100 000 famiglie del tipo MF, e’ ragionevole pensare che solo 1/2 dei padri mi parlera’ della figlia femmina l’altra meta’ mi dira’ di avere un figlio maschio $\rightarrow$ solo 50 000 famiglie di tipo MF vengono aggiunte al mio taccuino
• da 100 000 famiglie del tipo FM $\rightarrow$ 50 000 famiglie anche in questo caso solo la meta’ dei padri parlera’ della femmina
• da 100 000 famiglie del tipo FF $\rightarrow$ 100 000 famiglie: siamo certi che, se il padre parla di un solo figlio, dovra’ dire che ha almeno una femmina!

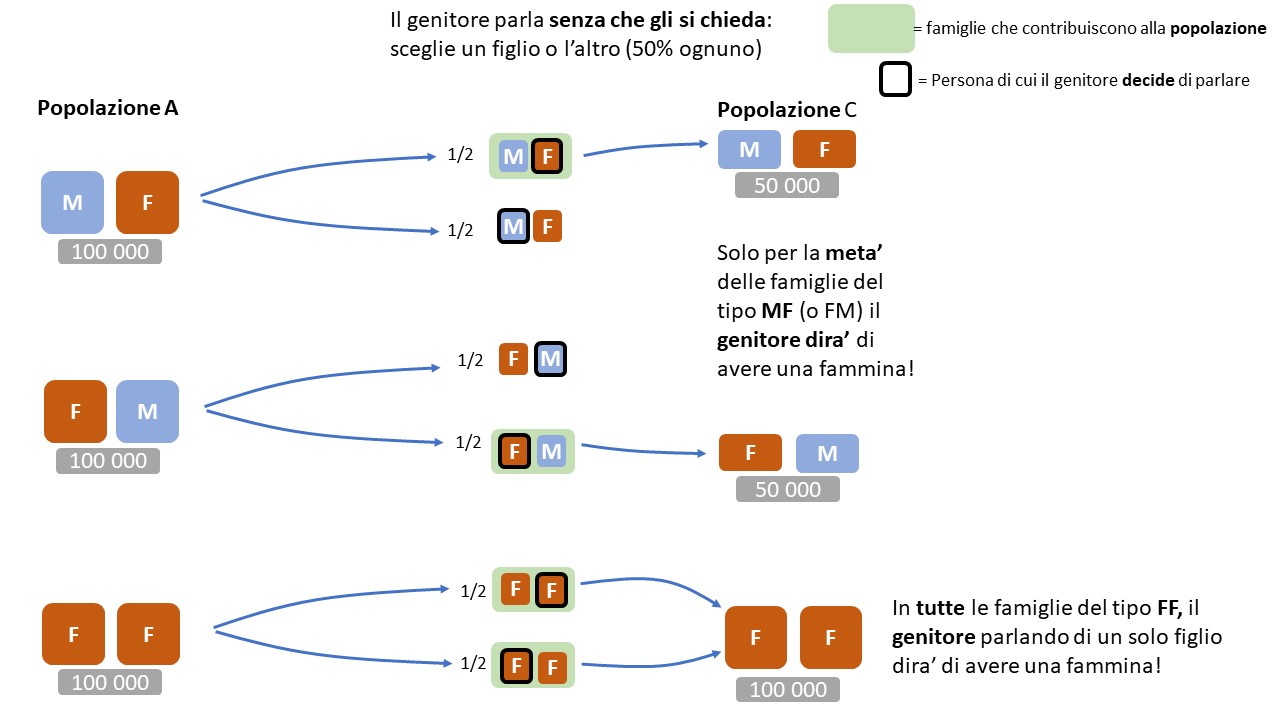
Quindi se io lascio che l’interlocutore decida di cosa parlare, invece di ottenere la popolazione A si ha la popolazione C:

• 50 000 famiglie del tipo MF
• 50 000 famiglie del tipo FM
• 100 000 famiglie del tipo FF

Notiamo subito una cosa:

• se chiedo attivamente informazioni riguardo alla famiglia ottengo un numero totale di famiglie segnato sul mio taccuino uguale a 300 000 (popolazione A).
• Se invece lascio lascio l’iniziativa di parlare al padre ottengo segnero’ sul taccuino una popolazione totale di sole 200 000 famiglie (popolazione C).

Per questo motivo se non si fa un campionamento attivo, quando si incontra Tizio al bar e questi ci dice che ha 2 figli di cui almeno uno femmina, la probabilita’ che anche l’altro figlio sia femmina e’ 1/2.

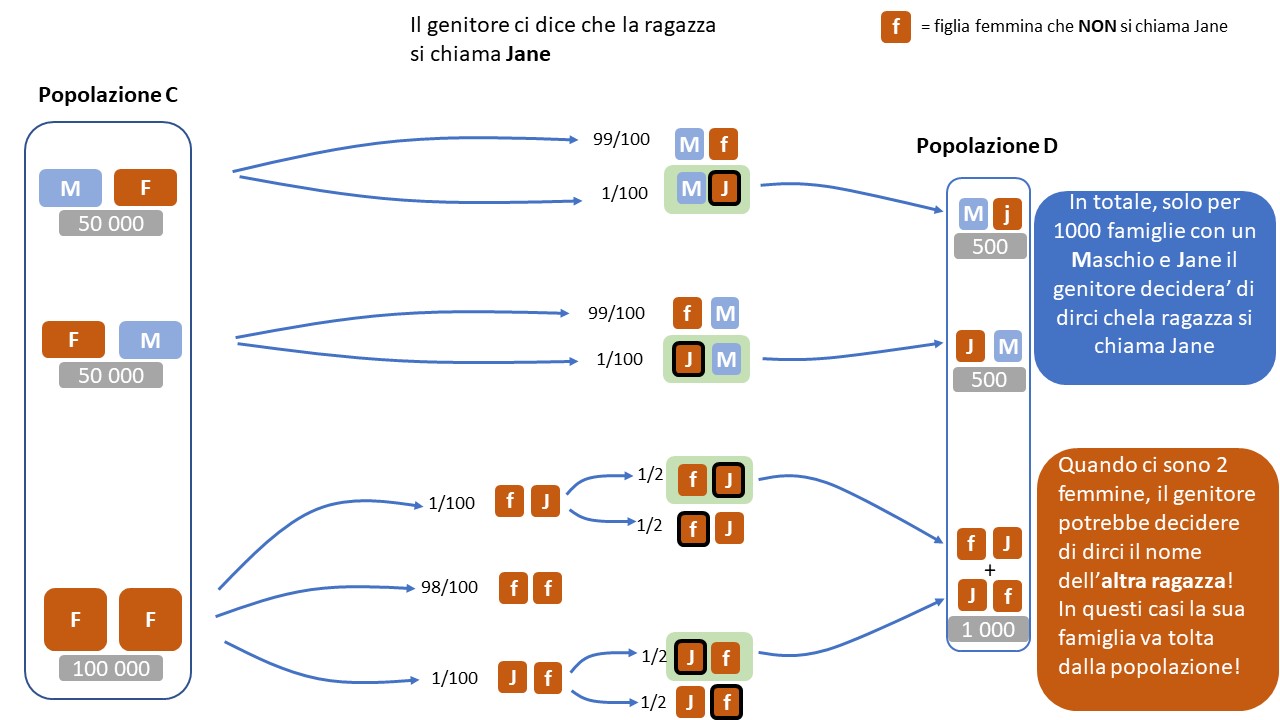
Popolazione D

Vediamo ora cosa succede (partendo dalla popolazione C) lasciamo che Tizio ci indichi (o meno) che il nome della propria figlia e’ Jane (nome con un’occorrenza ipotetica di 1/100), chiamo questo insieme di famiglie popolazione D (sottoinsieme della popolazione C):

• da 50 000 famiglie MF si passa a 500 famiglie MJ
• da 50 000 famiglie FM si passa a 500 famiglie JM
• da 100 000 famiglie FF si passa a 1000 famiglie composte la meta’ da Jf e l’altra meta’ da fJ (non e’ possibile dare lo stesso nome a due figli…)

In questo caso e’ interessante notare che un genitore con 2 figlie femmine, di cui una chiamata Jane, potrebbe decidere di dirci il nome dell’altra figlia (50% dei casi). Per questo, nonostante la sua famiglia rientri nelle caratteristiche che noi vorremmo, verra’ rimossa dalla popolazione totale perche’ lui ha deciso di rivelarci un’altra informazione!

In questo caso, il fatto che il genitore mi abbia indicato il nome della figlia non ha cambiato la probabilita’ che la seconda figlia sia femmina: resta 1/2.

Quando succede?

E’ questo un discorso questo di lana caprina? No! se effettivamente potessimo fare un esperimento del genere e scommettessimo dei soldi sul sesso dell’altro figlio di un nostro interlocutore, potremmo vincere (in media, ripetendo l’esperimento molte volte) solo chiedendo ATTIVAMENTE delle informazioni sulla sua famiglia. Altrimenti, lasciando all’interlocutore l’iniziativa di parlare e scommettendo sul sesso dell’altro figlio avremmo il 50% delle probabilita’ di azzeccare.

Conclusioni

Il modo in cui l’informazione viene raccolta (come si fa l’esperimento per un fisico) modifica in modo sostanziale la risposta. Non e’ una cosa nuova. Tutti sanno, per esempio, che per studiare una popolazione di qualche natura, non posso basarmi sui dati che mi vengono spontaneamente dati. Nel caso in questione, il fatto di chiedere attivamente all’interlocutore informazioni riguardo i propri figli, modifica quello che lui ci dira’. Nel caso di domande attive, le probabilita’ ottenute saranno quindi:

• 1/3 di coloro che ci dicono di avere una figlia femmina avra’ anche un’altra figlia femmina
• 1/2 di coloro che ci dicono di avere una figlia di nome Jane avra’ anche un’altra figlia femmina.

Se invece si registrano le informazioni fornite spontaneamente, anche se l’informazione fornita dall’interlocutore e’ la stessa rispetto al caso precedente, otterremo:

• 1/2 di coloro che ci dicono di avere una figlia femmina avra’ anche un’altra figlia femmina
• 1/2 di coloro che ci dicono di avere una figlia di nome Jane avra’ anche un’altra figlia femmina.

Quindi il motivo per cui la probabilita’ (nel caso di domanda attiva) e’ differente nei 2 casi e’ perche’ io seleziono delle famiglie particolari creando delle popolazioni specifiche. Nel dettaglio, selezionare le famiglie con almeno una figlia femmina di nome Jane privilegia le famiglie con 2 femmine. Per questo motivo la probabilita’ che anche il secondo figlio sia femmina passa da 1/3 a 1/2.

Detto in altri termini, le popolazioni usate per ottenere le probabilita’ cambiano a seconda che l’informazione venga data spontaneamente o meno. Questo perche’ il padre di due figli di cui uno e’ maschio e uno femmina, potrebbe spontanemente decidere di parlarci del figlio maschio. Il risultato sarebbe che la sua famiglia verrebbe automaticamente esclusa dalla popolazione totale e quindi questo cambierebbe le probabilita’ finali!

P.S: probabilmente in un altro post descrivero’ cosa succede nel caso in cui ci sia del rumore e l’informazione non venga passata correttamente.

P.P.S: Una considerazione da fisico, questo tipo di fenomeno ricorda curiosamente il problema della misura in meccanica quantistica. L’evoluzione spontanea di un sistema e’ profondamente differente dall’evoluzione dove interviene una misura.