Pytorch 7 Recurrent Neural Network
Posted on 17/10/2021, in Italiano. Reading time: 27 minsIndice Globale degli argomenti tra i vari post:
1.1. Indice degli argomenti.
1.1. Introduzione e fonti.
1.1. Lingo - Gergo utilizzato.
1.2. Tensori in Pytorch.
2.1. Chainrule e Autograd.
2.2. Backpropagation.
3.1. Loss e optimizer.
3.2. Modelli di Pytorch.
3.3. Dataset e Dataloader.
3.4. Dataset Transforms.
3.5. Softmax e Cross-Entropy Loss.
3.6. Activation Function.
4.1. Feed Forward Neural Network.
5.1. Convolutional Neural Network.
5.2. Transfer Learning.
5.3. Tensorboard.
6.1. I/O Saving and Loading Models.
7.1. Recurrent Neural Networks.
7.2. RNN, GRU e LSTM.
8.1. Pytorch Lightning.
8.2. LR Scheduler.
9.1. Autoencoder.
Recurrent Neural Network
Video, note e diapositive di Python Engineer.
Lezione del MIT sulle RNN
© Alexander Amini and Ava Soleimany
MIT 6.S191: Introduction to Deep Learning
IntroToDeepLearning.com
Attenzione alla notazione: il hidden-tensor non e’ un hidden layer del modello! E’ un tensore che viene usato per la predizione ma non e’ l’input!
Nota descrivo con qualche immagine in piu’ le RNN, LSTM e RCU nel prossimo capitolo.
Scopo: costruire una rete neurale ricorrente RNN, che prenda una dopo l’altra le singole lettere di un nome (ogni lettera sara’ un input) e alla fine dell’ultima lettera dica a quale lingua appartiene il nome
- usiamo batch di dimensione 1 qui (1 lettera)
LOGICA
- un nome e’ una sequenza di lettere.
- ogni lettera vine trasformata in un tensore-lettera che diventa
partedell’input della rete neurale. - Perche’ ho scritto solo
partedell’input? Perche’ l’input e’ una concatenazione di un tensore-lettera e un tensore-hidden! - la rete neurale restituisce in output a quale lingua appartiene la lettera … ma dato che in input c’e’ anche il tensore-hidden modificato dallo strato lineare (hidden tensor), c’e’ memoria delle lettere precedenti, quindi ha senso dire la lingua di appartenenza di una sola lettera: c’e’ comunque la memoria derivante dalle altre lettere ottenuta tramite il tensore hidden!
- come secondo output la rete neurale emette anche un nuovo tensore-hidden (che verra’ usato al passo successivo, concatenandolo al tensore-lettera successivo)
- alla fine della parola mi deve dire di che lingua stiamo parlando.
Le parole sono spezzate in modo da diventare sequenze di tensori, secondo la logica one-hot encoderd. Supponiamo di avere un alfabeto di 6 lettere: a, e, i, o, u, l.
La parola aiuola diventa la seguente sequenza di tensori 1D contennti 6 ingressi:
a= \(\left( \begin{eqnarray} {\bf 1} \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{eqnarray} \right)\) , i= \(\left( \begin{eqnarray} 0 \\ 0 \\ {\bf 1} \\ 0 \\ 0 \\ 0 \\ \end{eqnarray} \right)\) , u= \(\left( \begin{eqnarray} 0 \\ 0 \\ 0 \\ 0 \\ {\bf 1} \\ 0 \\ \end{eqnarray} \right)\) , o= \(\left( \begin{eqnarray} 0 \\ 0 \\ 0 \\ {\bf 1} \\ 0 \\ 0 \\ \end{eqnarray} \right)\) , l= \(\left( \begin{eqnarray} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ {\bf 1} \\ \end{eqnarray} \right)\) , a= \(\left( \begin{eqnarray} {\bf 1} \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{eqnarray} \right)\)
Quanto appena fatto e’ un tipo di embedding, ovvero una trasformazione da un dominio (quello delle lettere in questo caso) ad un
formato matematico (di grandezza fissa) che puo’ essere processato dalle reti neurali. Chiaramente esistono molti tipi di embedding
differenti e possono avere un impatto importante sui risultati.
Il tensore hidden invece ha una dimensione che fissiamo noi (nell’esempio 128), al passo 0 viene inizializzato con tutti 0,
ma ai passi successivi si popola perche’ lo strato lineare che costruisce le versioni successive del tensore hidden prende in ingresso sia il tensore combinato che il tensore della lettera. Per esempio se la lettera passata e’ la $a$ e il tensore-hidden e’:
hidden =
\(\left( \begin{eqnarray}
{\bf 0.3} \\
0.23 \\
\dots \\
0.29 \\
0.52 \\
0.11 \\
\end{eqnarray}
\right)\)
\(\begin{eqnarray}
1 \\
2 \\
\dots \\
126 \\
127 \\
128 \\
\end{eqnarray}\)
Allora il tensore-combinato = \(\left(\begin{eqnarray} {\bf a} \\ {\bf hidden} \\ \end{eqnarray} \right)\) = \($\left( \begin{eqnarray} {\bf 1} \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ {\bf 0.3} \\ 0.23 \\ \dots \\ 0.29 \\ 0.52 \\ 0.11 \\ \end{eqnarray} \right)\) (in questo esempio il tensore combinato ha dimensione 6 + 128 (perche’ in questo esempio l’alfabeto per l’one-hot encoring contiene solo aeioul, mentre la dimensione del tensore combinato nel video di Python Engineer e’ 57 +128, perche’ l’alfabeto da lui usato contiene tutte le maiuscole, le minuscole e alcuni segni di punteggiatura.
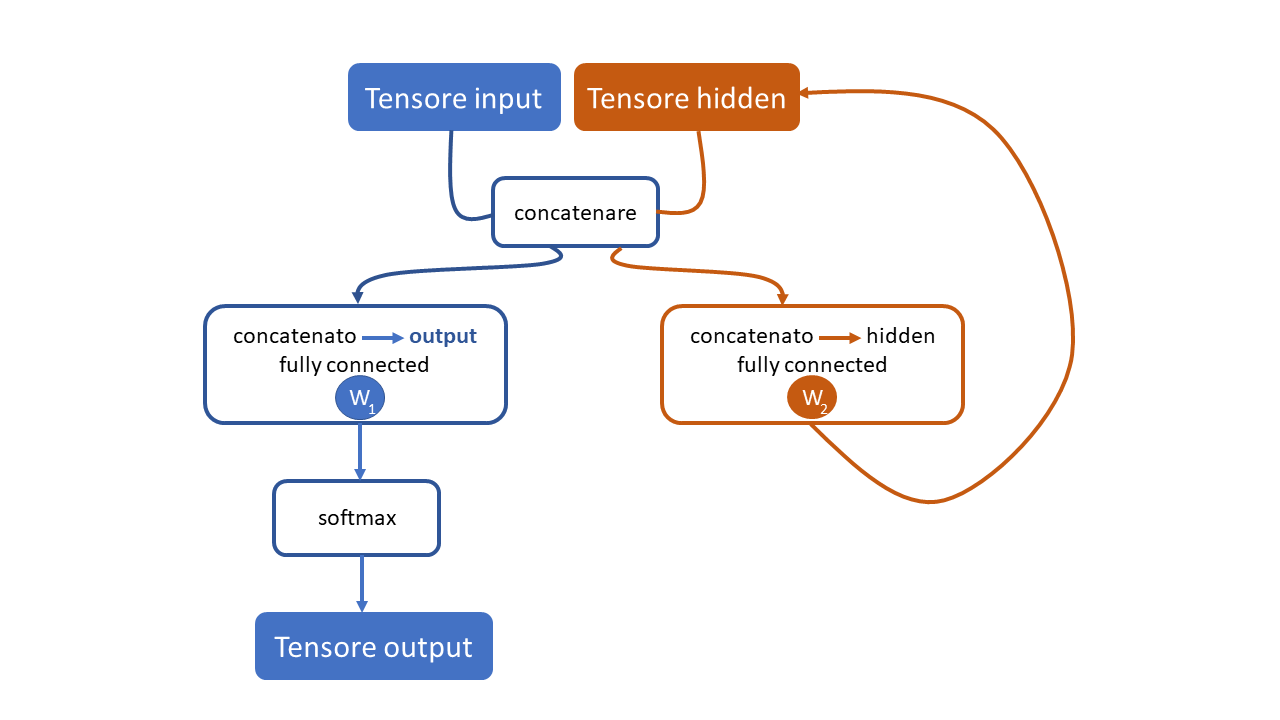
Osservazione
Il tensore che viene dato in pasto alla fully connected layer e’ la versione concatenata di:
- one-shot encoded (che ha dim 57 nel nostro caso, le maiuscole, minuscole e qualche segno di punteggiatura
- hidden tensor (che ha dimensione 128, perche’ lo abbiamo scelto noi).
Questo tensore concatenato viene dato in pasto anche ad un’altra fully connected layer in modo da mantenere la memoria di quanto e’ successo.
Nel video del MIT si dice che per fare il training di una RNN si usano la cosiddetta: BPTT (Backpropagation through time)
occhio che nel nostro caso non mi pare che si faccia. Nel dettaglio la backpropagation si fa sulla loss soltanto, e quindi l’hidden tensor e’ considerato come un input non come un peso. Per questo non mi e’ chiaro come venga aggiornato il tensore dei pesi che ho chiamato W2 nell’immagine.
PROBLEMI
-
ho provato a mandare tutto sul device CUDA ma rallenta! sospetto che sia perche’ copio sul device di volta in volta. Il tempo che impiega (su 5000 passi) e’ 23 s col device e 13 sulla cpu! Vediamo se riesco ad evitare di copiare le cose in GPU ogni passaggio per velocizzare il calcolo. Mettendo line_tensor e hidden prima ho guadagnao, ora sono 20 s (comunque piu’ lento che con la CPU)
-
Che strano: rifacendolo andare qualche giorno successivo ci mette 307 secondi! (sulla CPU) e se provo a farlo andare sulla GPU dice che ci sono problemiperche’ alcune cose sono su CPU e altre su GPU. Seguendo le indicazioni ho messo line_tensor.to(device) e ora sembra fungere linea 188.
-
ho inserito tutto fino a quando fa “whole sequence/name” ma ottengo un errore non ben chiaro: “IndexError: Dimension out of range (expected to be in range of [-1, 0], but got 1)”. Errore trovato: avevo scritto
inout_tensorinvece cheinput_tensor -
Il tensore in uscita ha dimensione 128 invece che 18 (il numero di lingue) e non capisco perche’! Chiaro avevo scritto:
self.i2o = nn.Linear(input_size + hidden_size , hidden_size)che quindi mi dava come dimensione di uscita del layer linearehidden_sizeinvece cheoutput_size!
Note:
Nella lezione si fa uso di funzioni di aiuto “helper functions” (io all’inizio capivo alpha-functions…). Python Engineer le mette in un modulo, mentre io le ho riscritte all’inizio del codice qui sotto
# dati https://download.pytorch.org/tutorial/data.zip
import io
import os
import unicodedata
import string
import glob # ?
import torch
import random
# Helper Functions
# Alfabeto minuscolo e maiuscolo
ALL_LETTERS = string.ascii_letters + ".,;''" # insieme delle lettere e della punteggiatura usata
N_LETTERS = len(ALL_LETTERS)
# converti un UNICODE in ASCII grazie a https://www.stackoverflow.com/a/518232/2809427
# in pratica trasforma le lettere accentate in lettere NON accentate
def unicode_to_ascii(s):
return ''.join( c for c in unicodedata.normalize('NFD',s) if unicodedata.category(c) != "Mn" and c in ALL_LETTERS)
# costuisce un dizionario "category_lines" e una lista di nomi per le varie lingue
def load_data():
category_lines = {} # dizionario
all_categories = []
def find_files(path):
return glob.glob(path) # glob??? The glob module finds all the pathnames matching a specified pattern according to ...
# leggi un file e spezzalo in linee
def read_lines(filename):
lines = io.open(filename, encoding='utf-8').read().strip().split('\n')
return [unicode_to_ascii(line) for line in lines]
for filename in find_files('data/names/*.txt'):
category = os.path.splitext(os.path.basename(filename))[0]
all_categories.append(category)
lines = read_lines(filename)
category_lines[category] =lines
return category_lines, all_categories
# trova l'indice di posizione associato ad una lettera nalla parola
def letter_to_index(letter):
return ALL_LETTERS.find(letter)
# trasforma una lettera in un tensore 1 x n letters (tensore riga)
def letter_to_tensor(letter):
tensor =torch.zeros(1, N_LETTERS)
tensor[0][letter_to_index(letter)]=1
return tensor
# trasforma una linea in una <line_length x 1 x n_letters>
# o un array hon-hot letter
def line_to_tensor(line):
tensor = torch.zeros(len(line), 1, N_LETTERS)
for i, letter in enumerate(line):
tensor[i][0][letter_to_index(letter)]=1
return tensor
def random_training_example(category_lines, all_categories):
def random_choice(a):
random_idx = random.randint(0,len(a)-1)
return a[random_idx]
category = random_choice(all_categories)
line =random_choice(category_lines[category])
category_tensor = torch.tensor([all_categories.index(category)], dtype=torch.long)
line_tensor = line_to_tensor(line)
return category, line, category_tensor, line_tensor
###############################################################################
###############################################################################
###############################################################################
#print(ALL_LETTERS)
#category_lines , all_categories = load_data()
#print(category_lines['Italian'][:5])
#print(letter_to_tensor('J')) # trasforma la lettera J (maiuscola) in un tensore one-hot encoding (sono 1D con 57 ingressi)
#print(line_to_tensor('Jones').size()) # Jones contiene 5 lettere, ognuna e' trasformata in un tensore 1D con 57 ingressi
#test = line_to_tensor('Jones')
#print(test)
################## ok sopra funge correttamente ###################
# ho gia'importato torch sopra
import torch.nn as nn
import matplotlib.pyplot as plt
import time
# from utils import ALL_LETTERS, N_LETTERS # qui non serve perche' fanno gia' parte di questo listato
# from load_data, letter_to_tensor, ...
#device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
device = torch.device('cpu')
# esiste gia' un RNN in Torch, qui pero' lo creiamo da zero.
class RNN(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(RNN, self).__init__()
self.hidden_size = hidden_size
self.i2h = nn.Linear(input_size + hidden_size , hidden_size) # ricorda che servono solo le dimensioni: dim tensore combinato, dim uscita
self.i2o = nn.Linear(input_size + hidden_size , output_size) # input 2 output
self.softmax = nn.LogSoftmax(dim=1) # input ha dimensione 1,57, quindi softmax sulle colonne
def forward (self, input_tensor, hidden_tensor):
combined = torch.cat((input_tensor, hidden_tensor ),1) #concatena input tensor e hidden tensor: nuova dimensione= input_size+hidden_size
hidden = self.i2h(combined) # qui spara fuori l'oggetto hidden, i pesi di questo layer non sono l'oggetto hidden!
output = self.i2o(combined) # qui indica la guess riguardo la nazione
output = self.softmax(output) # qui usa la softmax per ottenere valori di probabilita'
return output, hidden # restituisce sia l'output che l'hidden per il prossimo passo
def init_hidden(self): # inizializza lo hidden_tensor alla dimensione hidden_size
return torch.zeros(1, self.hidden_size)
category_lines, all_categories = load_data() # chiave valore, nazione chiave, nome valore, e poi tutte le nazioni
n_categories = len(all_categories)
#print(n_categories)
n_hidden =128 # selto da me
rnn = RNN(N_LETTERS, n_hidden, n_categories).to(device) # qui ho inizializzato il modello, servono i parametri del costruttore
# likelyhood di ogni nazione, vogliamo l'indice della categoria massima
def category_from_output(output):
category_idx = torch.argmax(output).item()
return all_categories[category_idx]
#print(category_from_output(output))
#print(output)
####### facciamo il training ######
criterion = nn.NLLLoss() # negative log likelihood loss
learning_rate = 0.005 #
optimizer = torch.optim.SGD(rnn.parameters(), lr=learning_rate)
# funzione helper che fa il training metto il tensore e la sua label
def train(line_tensor, category_tensor):
hidden = rnn.init_hidden().to(device) # azzero l'hidden tensor iniziale
# hidden = hidden.to(device)
#line_tensor = line_tensor.to(device)
for i in range (line_tensor.size()[0]):
# lunghezza del nome
#l2d = line_tensor[i].to(device)
# output, hidden = rnn(l2d, hidden)
output, hidden = rnn(line_tensor[i], hidden) # inserisco i 2 tensori di input: lettera one-shot e hidden
category_tensor = category_tensor.to(device)
#output = output.to(device) # inventato da me ma da comunque errore
loss = criterion(output, category_tensor)
optimizer.zero_grad()
loss.backward()
optimizer.step()
return output, loss.item()
current_loss = 0
all_losses = []
plot_steps, print_steps = 100000, 100000
n_iters = 100000
since = time.time() # il momento d'inizio
for i in range (n_iters):
category, line, category_tensor, line_tensor = random_training_example(category_lines, all_categories)
line_tensor = line_tensor.to(device)
output, loss = train(line_tensor, category_tensor)
current_loss += loss
if (i+1)% plot_steps == 0:
all_losses.append(current_loss /plot_steps)
current_loss =0
if (i+1)% print_steps ==0:
guess = category_from_output (output)
correct = "Corretto" if guess == category else f" Sbagliato ( {category})"
print (f'{i} {i/n_iters*100} {loss:.4f} {line}/{guess}{correct} ' )
if (i+1)% 100000 ==0:
print('Tempo impiegato ', time.time() -since)
#plt.figure()
#plt.plot(all_losses)
############# data una stringa in ingresso
def predict(input_line):
print(f'\n> {input_line}') # la riscrive
with torch.no_grad():
line_tensor = line_to_tensor(input_line) # trasforma in un tensore
hidden = rnn.init_hidden() # crea lo stato iniziale vuoto da dare in pasto
for i in range (line_tensor.size()[0]): # gira sui tensori one-hot encoded
output, hidden = rnn(line_tensor[i], hidden) # usa la rete neurale, uno dietro l'altro, cosi' hidden si aggiorna
guess = category_from_output(output) # Ottiene dal numero il nome della nazione
print(guess) # stampa il nome della nazione
########## qui si imparano molte cose #######
while True:
sentence = input("Inserisci un nome (quit per terminare)") # scrive a video
if sentence == 'quit': # esci dal ciclo se scrivi quit
break
predict(sentence) # usa la rete neurale e scrivi la predizione
99999 99.99900000000001 1.3037 Woo/Chinese Sbagliato ( Korean)
Tempo impiegato 319.30727434158325
Inserisci un nome (quit per terminare)quit
RNN, GRU e LSTM
Il video di Python Enginner contiene un esempio di RNN. E’ basato fortemente sulle note di PyTorch.
Recurrent Neural Networks cheatsheet di Stanford e’ molto completa e succinta! Probabilmente e’ la guida piu’ precisa, la matematica usa delle notazioni diverse dalle altre due (per esempio l’hidden tensor viene indicato con a), ma suppongo che sia la piu’ affidabile.
In questa guida illustrata delle LSTM e dell GRU si cerca di non mettere la matematica, ma ci sono delle gif animate.
In questa pagina vengono indicate anche le formule associate ai vari passaggi; ma sospetto che le formule non corrispondano alle immagini (ha preso le immagini da qualche parte e le formule altrove). Di buono mette anche le formule per la backpropagation!
Il Codice
Qui usiamo i moduli gia’ creati per Long Short Term Memory e per GRU. Si prende come punto di partenza il tutorial 13 di Python Engineer.
Invece che guardare a tutta una immagine per volta vogliamo prendere una sequenza di righe
Usiamo Architettura Many to 1 (molti input e un solo output)
Commentando e decommentando le parti con GRU e LSTM si ottengono tutte e 3 le architetture. In realta’ sono solo 2 le righe che vanno cambiate tra GRU e RNN e 3 per LSTM (si deve mettere anche la cella)!
Nel codice qui sotto si fa una sorta di estensione rispetto al lavoro fatto nel capitolo 13 (Feed Forward NN )
RNN di torch.nn.RNN e’ una Elman:
\(\large
\displaystyle
h_t = \tanh\left( \frac{} {}
W_{ih} x_t +b_{ih} + W_{hh} h_{t-1}+b_hh
\right)\)
- $h_t$ hidden state al tempo $t$
- $h_{t-1}$ hidden state al tempo $t-1$ (eh… abbastanza ovvio)
- $x_t$ input al tempo $t$
- $W_{ih}$ sono i pesi che contribuiscono a $h_t$ dal tensore di input $x_t$
- $b_{ih}$ sono i
biasche contribuiscono a $h_t$ dal tensore di input - $W_{hh}$ sono i pesi che contribuiscono a
- $b_{hh}$ sono i
bias(non chiaro perche’ vengano distinti rispetto a b_{ih}, alla fine sono delle costanti… - $x_t$ vettore di input al tempo t
- $\hat{y}_t$ vettore di output al tempo t
- $y_t$ le label vere (ground truth) al tempo t
Empirical Loss:
- Quando si ha una RNN si hanno diversi output per ognuno dei “tempi” t
- Si sommano i valori delle loss.
ok a questo punto pero’ dovrebbero anche esserci i pesi per l’output, nella formula sopra vedo solo l’equazione per l’hidden state.
Vediamo un grafico per LSTM:
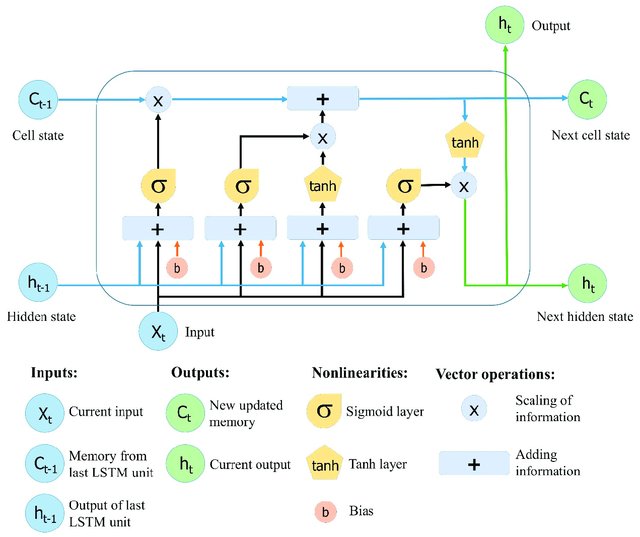
import numpy as np
import torch
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
%matplotlib inline
# device config
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
#device = torch.device('cpu')
# Hyper parametri
#input_size = 28*28 # =784 sono le dimensioni delle immagini
hidden_size = 128 # scelto da me
num_classes = 10 # devo classificare immagini di numeri
num_epochs = 2 # quanti giri completi vengono fatti
batch_size = 100 # questo no so come sia stato scelto
learning_rate = 0.001 # piccolo
input_size = 28 # singolo input e' la riga RNN
sequence_length =28 # ci sono 28 righe RNN
num_layers = 2 # di default =1 RNN
train_dataset = torchvision.datasets.MNIST(root= './data/', train= True,
transform =transforms.ToTensor(),
download = True)
test_dataset = torchvision.datasets.MNIST(root= './data/', train= False,
transform =transforms.ToTensor(),
download = False) #
train_loader = torch.utils.data.DataLoader(dataset= train_dataset, batch_size = batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader (dataset= test_dataset, batch_size = batch_size, shuffle=False)
### nota che la dimensione dei sample e' la seguente
# 100 = numero di immagini nel batch (se non metti batch_size, di default vale 1)
# 1 = numero di canali solitamente i colori
# 28 = numero di ingressi sull'asse delle x
# 28 = numero di ingressi sull'asse delle y
############ MODELLO ####################
class RNN(nn.Module):
def __init__(self, input_size, hidden_size, num_layers, num_classes):
super(RNN, self).__init__()
self.num_layers = num_layers # RNN
self.hidden_size = hidden_size # RNN
#self.rnn = nn.RNN(input_size, hidden_size, num_layers, batch_first=True) # RNN , l'ordine e' importante batch set first dimension RNN
#self.gru = nn.GRU(input_size, hidden_size, num_layers, batch_first=True) # GRU
self.lstm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True) # LSTM
# x -> batch_size, seq, input_size
self.fc = nn.Linear(hidden_size, num_classes) # RNN questo e' per l'ultimo passo della sequenza per avere la classificazione
# RNN da documentazione ora servono 2 input, uno e' lo stato e l'altro e' l'hidden state
def forward (self, x):
h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(device) # RNN numero di layer, batch size, hidden size
c0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(device) # LSTM initial cell
#out, _ = self.rnn(x, h0) # RNN restituisce 2 outputs, uno out e hidden state per step n
#out, _ = self.gru(x, h0) # GRU restituisce 2 outputs, uno out e hidden state per step n
out, _ = self.lstm(x, (h0,c0)) # LSTM restituisce 2 outputs, uno out e hidden state per step n
# RNN batch_size, sequence_length, hidden_size
# RNN vogliamo l'hidden state dell'ultimo step
# RNN out (N, 28, 28)
out = out[:, -1, :] # RNN serve solo l'ultimo time step quindi metto -1 e tutte le feature dell'hidden size
# RNN out(N, 128)
out = self.fc (out) # RNN
return out
############### ISTANZIO MODELLO, Loss, optimizer ########
model = RNN(input_size, hidden_size, num_layers, num_classes).to(device)
criterion = nn.CrossEntropyLoss() #
optimizer = torch.optim.Adam(model.parameters(), lr = learning_rate) #
n_total_steps = len(train_loader)
for epoch in range(num_epochs): #
for i, (images,labels) in enumerate (train_loader): #
# 100, 1, 28, 28 (batch, canali, x, y) forma del tensore images
# 100, 28x28=784 forma voluta dall'hidden layer
images = images.reshape(-1, sequence_length, input_size).to(device) # Ora vogliamo solo righe e tante.
labels = labels.to(device)
outputs = model (images) # non chiama il metodo forward: perche'?
loss = criterion(outputs, labels)
# backward pass
optimizer.zero_grad() #
loss.backward() #
optimizer.step() #
if (i+1) % 100 ==0:
print(f'epoch {epoch+1} / {num_epochs}, step {i+1}/{n_total_steps}, loss= {loss.item():.4f}')
############ TEST LOOP e' identico a RNN e FeedForward! #################
with torch.no_grad():
n_correct = 0 # numero di predizioni azzeccate
n_samples = 0 # ?
for images, labels in test_loader:
images = images.reshape(-1,sequence_length, input_size).to(device)
labels = labels.to(device)
outputs = model(images) # qui il modello e' gia' trainato!
_, predictions = torch.max(outputs,1) # prendo la classe che ha il valore massimo
n_samples += labels.shape[0] # numero di samples nel batch corrente (nell'ultimo sono diversi spesso)
n_correct += (predictions == labels).sum().item()
acc = 100.0 * n_correct / n_samples # accuratezza in percentuale
print(f'accuracy ={acc}')
epoch 1 / 2, step 100/600, loss= 0.9440
epoch 1 / 2, step 200/600, loss= 0.5394
epoch 1 / 2, step 300/600, loss= 0.3369
epoch 1 / 2, step 400/600, loss= 0.1903
epoch 1 / 2, step 500/600, loss= 0.2440
epoch 1 / 2, step 600/600, loss= 0.1913
epoch 2 / 2, step 100/600, loss= 0.1267
epoch 2 / 2, step 200/600, loss= 0.1024
epoch 2 / 2, step 300/600, loss= 0.0285
epoch 2 / 2, step 400/600, loss= 0.1911
epoch 2 / 2, step 500/600, loss= 0.1058
epoch 2 / 2, step 600/600, loss= 0.1007
accuracy =97.46

Comments